Introduction
The pairing-based cryptography (PBC) differs considerably from the prior cryptosystems. It covers many novel cryptographic applications that are hard, if not impossible to construct with other known cryptographic primitives. The PBC is based on a special bilinear pairing -mapping, which takes two elliptic curve points and maps them into a single point in an extension field.
The concept of bilinear pairing was originally brought forth in 1993, in the form of MOV-attack which exploits the pairings to attack the elliptic curve cryptosystems that utilize a specific class of curves. However, after two decades of research, it has turned out that the pairings can be used to construct innovative cryptographic applications, such as ID-based encryption and signatures, privacy-aware group signatures and searchable encryption.
A major bottleneck in the pairing implementations is posed by the massive runtime and resource requirements of the involved computations. In this thesis work, the bilinear pairing, and related functions of PBC were benchmarked on nRF9160 microcontroller with 64 MHz Cortex-M33. A bare-metal solution based on an opensource library was used, with certain optimizations made to support 64-bit multiplication of the M33. The pairing-function was effectively computed in 410ms, resulting in limited, but applicable usage of pairing-based cryptography.
Bilinear Pairings
The computations of bilinear pairings involve quite advanced level mathematics and complex computations. Therefore the self-containing representation is out of question. In this section, the concept of bilinear pairings is outlined in a highly compressed format. Good free sources about pairings exists, mentioned at the end, which can be referred for deeper understanding.
A bilinear pairing is a mapping based on groups formed by elliptic curves over extension fields. The elliptic curve in our case is defined as y^2=x^3+2 (modulo the size of the extension field), where the x,y are elements of a large extension field. The curve points, i.e. tuples (x,y) satisfying the equation form the elliptic curve group. This kind of elliptic curve group over a field with a size of over 2^256 elements are used as the arguments in bilinear pairings.
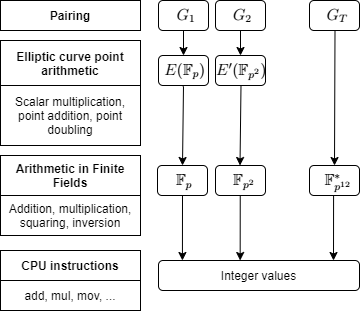
As mentioned, the bilinear pairing -function, e(P,Q) G1xG2--> GT, takes two points from elliptic curve groups as the arguments and maps them to a single finite-field element. The bilinearity means that for any P, Q in G1 and T, S in G2: e(P+Q,T)=e(P,T)e(Q,T) and e(P,T+S)=e(P,T)e(P,S). I.e. the bilinear pairing is linear for both arguments. The G1 and G2 are the used elliptic curve groups. The pairing is also non-degenerate, i.e. for any P in G1 exists Q in G2 such that e(P,Q) != 1 and for any Q in G2 exists P in G1 such that e(P,Q) != 1. It follows that for any scalars a,b and curve points P,Q: e(aP,bQ)=e(P,Q)^(ab). This expression is also equivalent to e(bP,aQ)=e(abP,Q)=e(aP,Q)^b=.. . Thus, the bilinearity enables the scalars to be swapped from group to another. This is the fundamental property that enables bilinear pairings for creating special cryptographic protocols.
The process of computing the bilinear pairing is quite complex. In general, the pairing function consists of two phases; evaluation of Miller's loop and the final exponentiation process. Both processes are computationally heavy, involving many multiplications, squaring, and exponentiations with large, up to 256bit elements. The pairing function used in the implementation is optimal ate-pairing, which is considered as the most efficient by the time. As the curve, BN254 (Barreto-Naehrig curve over 254-bit of size prime) is used, which provides certain efficient parametrization for curve points. Currently, the BN254 curve provides around 100 bits of security. The figure below describes the layered arithmetic of the used groups. The pairing computation breaks into arithmetic of elliptic curve points, which turn into finite field operations. These are, ultimately computed as big-integer operations as CPU instructions. A single ate-pairing with 128-bits of security requires around 17000 prime field multiplications.
The security of elliptic-curve based cryptography relies on the discrete logarithm problem (DLP) over curve-point arithmetic: for known elliptic curve points P and Q, the task is to find the (secret) scalar k for which kP=Q. In elliptic curve groups with 2^256 elements and appropriate parameters, the most efficient solution for solving the DLP would require roughly 2^128 steps. This is the security basis for elliptic curve cryptography but also essential for bilinear pairings. In terms of bilinear pairings, a bilinear Diffie-Hellman (BDH) problem is another underlying structure. The task in BDH is to solve e(P,Q)^(ab) if P, aP, bP in G1, and Q in G2 are known. Currently, there exist no (known) attacks against optimal ate-pairing with appropriate parameters.
Applications
Many interesting applications are enabled by bilinear pairings, which of most are asymmetric cryptosystems, i.e. consisting of a public and private key. The applications include identity-based encryption, certificateless signatures, searchable encryption, privacy-aware group signatures, and signcryption (performs signing and encryption simultaneously). Some of the interesting applications are outlined below.
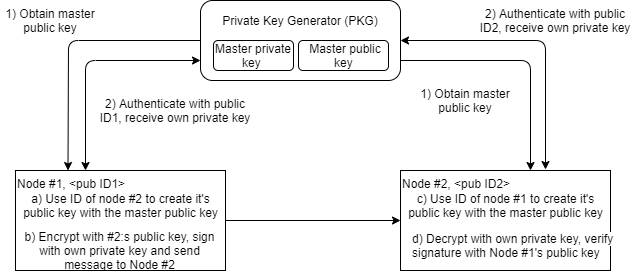
The identity-based encryption and certificateless signatures are based on the same idea. The public key of an attendee can be generated from a unique, identity-bound ASCII string (which is public information). The user first obtains a master public key from a Private Key Generator (PKG). She then authenticates herself to PKG with the corresponding ID, which provides her the user-specific private key, by using the ID and master private key. The public keys of all communication parties are obtained by combining the ID with the master public key. The protocol removes the need for certificates, which are used to verify the ownership of a certain public key. The ID-based cryptosystems are useful in cases where the pre-distribution of authenticated keys is inconvenient or infeasible due to technical restrictions. This example as-is has a certain key-escrow problem; i.e. the PKG knows ALL the secret keys. This problem although has a solution.
The searchable encryption enables the user to determine whether a certain string is included in encrypted data, without the need for decryption or revealing the search keyword. It removes the need for a secure channel, that was previously needed in a public key encryption with a search. The search can be carried out on a non-trusted server in a network.
The group signature scheme permits a member of a group to perform a signature on behalf of the group, in a way that any verifier of the signature can be convinced that the signature has been produced by a member of the group, but without knowing which of them. A designated authority can be determined, who can, if necessary, "open" the signature to identify the actual signer. The scheme can be used to provide user anonymity and user accountability simultaneously. Applications vary from anonymous credentials on mobile services to electronic voting (not deployed in practice yet). There exists also RSA based version of group-based signatures.
The new authentication mechanisms, group-based and privacy-preserving protocols might be especially useful in the context of interconnected, autonomous smart systems, and IoT. Several solutions have already been proposed in wearable technologies, the Industrial Internet of Things, health record systems, and sensor networks. The possibility of using bilinear pairings certainly needs to be studied, also in the embedded low-constraint platforms.
Implementation and Results
The implementation builds on open source library [1], which targets the ARM Cortex-M0+ architecture. The proposed library was built and analyzed on the nRF9160 DK as a bare-metal solution. The optimizations include optimized multiplication routines and code allocation to RAM. As the Cortex-M33 supports 64-bit multiplication instruction, the squaring, prime field reduction, and Karatsuba multiplication were optimized. For example, the cycle consumption of the Karatsuba-multiplier was decreased from 4580 to 2770 cycles. The instruction cache was effectively used in the implementation. However the instruction cache of nRF9160 is only 2048 bytes, and the frequently used Karatsuba multiplier and reduction algorithms exceeded it, resulting in numerous cache misses. We thus decided to allocate these algorithms to RAM, from which the instruction fetching is as fast as from instruction cache.
Initially, with the open source library as-is, a single optimal ate pairing took 50,768 kCycles. With the final optimized setup and compiler optimizations, a single pairing was effectively computed in 25,917 kCycles, or 410ms. Memory footprint is 15946 bytes of flash and 5386 bytes of RAM. The most efficient ID-based signature by the time of 2019 requires one EC point scalar multiplication for signature generation, and two pairings for verification. This would take 130 ms and 2*410=820 ms for corresponding operations. As a conclusion, the proposed implementation enables a limited usage of pairing-based cryptography. The protocol could be easily used for authentication, for example, when joining a sensor network and authenticating with base-station. Or performing a group signature for a certain infrequent action. The feasibility of this solution highly depends of the use-case of the cryptosystem.
Conclusions
The pairing was effectively computed in 410ms / 25917 kCycles, which is enough for use-cases that require infrequent computation of pairing, and the related operations. The result was the best among other low-power (<100 MHz) platforms. However, not many referencing results were found. Most of the implementations seem to favor either over 1GHz (and energy-consuming) CPU or external drop-in units (customized FPGA's) and other accelerators. The usage of FPGA or accelerators is one consideration for possible future improvements. Some comparisons can be found from the thesis document.
Also, the used curve (Barreto-Naehrig) is not considered to be the most efficient anymore. The Barreto-Lynn-Scott (BLS) curves seem to have bypassed BN curves in terms of efficiency. However, the chance of curve-type wouldn't bring significant improvement in performance. The usage of BLS would bring roughly 80ms improvement in the computation of ate-pairing. The performance of under 100ms would require an enhanced hardware-solution.
The proposed library is easily re-used and modified for other curve-types and improved Miller function or final exponentiation. The research on improving pairing-based cryptography is still in a phase of continuous research and improvement. It has not yet been accommodated as a stable tool for wide use. Progression is continuously made in every front-line; the pairing routines get improved, as well as the actual protocols.
Notable is that the library also supports the elliptic curve cryptography and has support for randomized curve points and side-channel protection. However, as it is based on open-source, it might require some security evaluation before deploying. Nonetheless, the results that are obtained with the current implementation show that the pairing-based cryptography certainly is practicable with Nordic devices and could be applied in the future.
Notes
For more details of the project, results and the topic itself, see the original thesis:
Performance Evaluation of Optimal Ate-Pairing on Low-Cost Single Microprocessor Platform:
https://www.utupub.fi/bitstream/handle/10024/150659/Pesonen_Mikko_opinnayte.pdf?sequence=1&isAllowed=y
Useful links
Link to the Github project: https://github.com/mhspes/pairings_in_c
[1] Unterluggauer et al. (2014) Efficient Pairings and ECC for Embedded Systems: https://eprint.iacr.org/2014/800.pdf
Further reading:
Grewal Gurleen (2012) Efficient Pairings on Various Platforms: https://uwspace.uwaterloo.ca/bitstream/handle/10012/6722/Grewal_Gurleen.pdf?sequence=1&isAllowed=y (available free)
Graig Costello, Pairings for Beginners: http://www.craigcostello.com.au/pairings/PairingsForBeginners.pdf (available free)
Nadia El Mrabet, N., & Joye, M. (2017). Guide to Pairing-Based Cryptography. Chapman and Hall/CRC.




