125 kbps PHY Rx Sensitivity Not As Low As It Should Be

[GaryS]

Hi - 

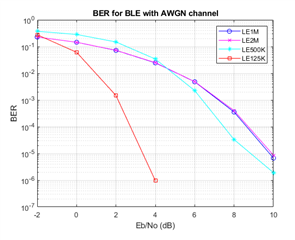
In reading through the data sheets for the Nordic chips that support the low-rate (125 kbps) BT 5 PHY, I'm seeing Rx sensitivity numbers around -103 dBm. For the 1 Mbps PHY, it's around -96 dBm. I would expect the Rx sensitivity for 125 kbps to be 12 dB lower than 1 Mbps, i.e., -96 - 12 = -108 dBm. 9 of the 12 dB comes from reducing the bit rate by 8x, the other 3 dB comes from coding gain added to the low rate S=8 PHY. Why are you guys leaving 5 dB on the table? This is a big miss, in my opinion, since 5 dB amounts to almost a 2x range increase outdoors!

Do you have any plans in the future to improve the PHY performance to make up for the 5 dB shortfall?

Thanks,

Gary Sugar

[Dmitry]

Hi Gary,

I'm not an expert in signal processing, but I don't think you can make a direct assumption from bitrate factor. Coded PHY uses exactly the same physical channel bitrate as 1M PHY - 1 mbit/s, so you get the same BER/SNR curve after GFSK demodulation. First stage (500k) is a convolutional encoder that let us survive with higher level of error rates (for uncoded, any error in a single bit means packet is completely lost). I couldn't find a right method to compare sensitivity for these two cases. This simulation shows an 1dBm gain, but it considers only physical layer. Anyway it would be interesting to simulate a decoder with a noisy channel to see which BER of underlying channel will match, say, 10^-3 after decoding.
At second stage (125k), each symbol is encoded with 4 bits - here you can expect a direct increase of sensitivity up to 6 dBm as by lowering bitrate, also it helps to suppress interference from adjacent channels.

[GaryS]

Thanks for sending this simulation link Dmitry - this is great and it helps me make my point. 

The plot below from the simulation shows that you get a 1e-3 BER at an Eb/N0 = 7 dB for LE1M, and 2 dB for LE125K. The Eb/N0 is the receiver's received energy per bit period (Eb) divided by the receiver's noise power spectral density. We can convert this to signal to noise ratio (SNR = signal power divided by noise power) by noting that SNR = (Eb/Tb) / (N0 * f0) = Eb/N0 * fb/f0, where Tb = 1/fb is the bit period in seconds, and f0 is the receiver's noise bandwidth in Hz. In dB, you get SNR (dB) = Eb/N0 (dB) + 10*log10(fb/f0). You can read about this relationship here. The bit rate is fb = 125 kbps for LE125K and 1 Mbps for LE1M. So the delta at BER = 1e-3 between the two schemes is 5 dB in Eb/N0, but it's 5 + 10*log(1M/125k) = 14 dB for SNR! This shows that the sensitivity for LE125K should be LE1M. The fact that it's not means the receiver is implemented sub-optimally.

Gary 

[GaryS]

Oops - I should have said "This shows that the sensitivity for LE125K should be 14 dB better than LE1M. ". 

[Dmitry]

GaryS said:

The bit rate is fb = 125 kbps for LE125K and 1 Mbps for LE1M

No, the bitrate is 1Mbps both for 1M and 125K. We have not a reducing of bitrate AND redundant encoding - we have a reducing of bitrate BECAUSE OF redundant encoding. The upper-layer encoding methods are quite different to consider them as simple lowering of bitrate. At physical layer, we have 5 dB between 1M and 125K, plus some gain given by convolutional encoding - I don't know the formula but it should include at least time on-air (crucial for CRC-protected 1M but almost irrelevant for coded stream).

[GaryS]

By bit rate, I mean information rate - the rate at which uncoded bits are sent over the channel. It doesn't include redundancy for FEC or the bandwidth expansion from 125 kbps to 1 Mbps. 

[Dmitry]

GaryS said:

By bit rate, I mean information rate - the rate at which uncoded bits are sent over the channel

The radio don't agree with you :) it just works at 1M. We could consider 1/8x bitrate (and expect +9 dBm) in case if we transmit each symbol 8x longer, use 1/8x narrower band filter and 8x more accurate clock.

[GaryS]

OK, so are you happy with the sensitivity for LE125kbps being only 7 dB less than it is for LE1M? If not, what do you think it should be? 

[Dmitry]

I would believe the online calculator from Bluetooth SIG that shows 7 dBm difference.